Основные уравнения движения газа в двигателях и их элементах
Движение воздуха или газа в элементах двигателя это сложное течение вязкого сжимаемого газа. В практике для анализа такого течения широко используются одномерные уравнения установившегося движения газа при следующих допущениях:
- движение газа считается стационарным (установившимся), т.е. параметры потока (скорость, давление, температура, плотность) в любой точке рассматриваемого объема считаются неизменными во времени;
- течение газа является одномерным, т.е. параметры потока во всех точках каждого поперечного сечения потока одинаковы; их изменение происходит лишь в направлении движения.
Уравнение неразрывности
Расход газа G через любое поперечное сечение какого-либо канала, т.е. количество газа, проходящее через это сечение в единицу времени, равен G = c·ρ·F , где с - скорость потока, ρ - его плотность, а F - площадь данного сечения.
На установившемся режиме расход газа через все сечения данного канала одинаков. Следовательно, для двух произвольных сечений 1-1 и 2-2 (рис. 1)
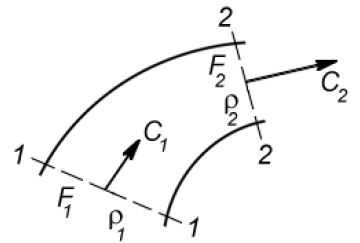
c1·ρ1·F1 = c2·ρ2·F2 или c·ρ·F = const .
Рисунок 1 - К составлению уравнения неразрывности
Уравнение сохранения энергии
Если к установившемуся потоку газа между сечениями 1-1 и 2-2 (рис. 2)
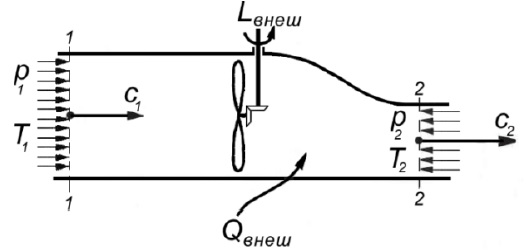
Рисунок 1 - К составлению уравнения сохранения энергии
подводится извне (в расчете на единицу массы) работа Lвнеш и теплота Qвнеш , то
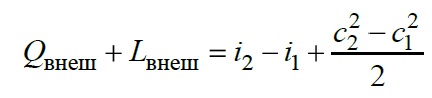
где i и с энтальпия единицы массы и скорость потока газа в соответствующих сечениях.
В параметрах заторможенного потока это уравнение имеет вид
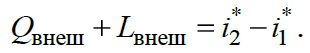
То есть теплота и работа, подведенные к газу, приводят к повышению его полной энтальпии.
Обобщенное уравнение Бернулли
Если из уравнения сохранения энергии вычесть уравнение первого закона термодинамики , то получим следующее уравнение
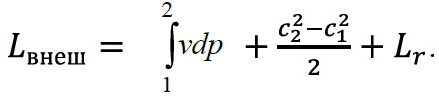
Это уравнение называется обобщенным уравнением Бернулли. Оно показывает, что подведенная к газу внешняя работа расходуется на его политропическое сжатие, изменение кинетической энергии и преодоление гидравлического сопротивления Lr.
Теорема Эйлера об изменении количества движения
При проектировании газотурбинных двигателей возникает необходимость определения сил взаимодействия газа с элементами двигателя, находящимися в потоке (например, при определении усилий, действующих на лопатки компрессора и турбины, силы тяги, создаваемой двигателем, и т.д.).
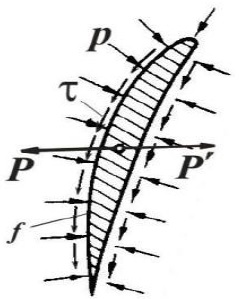
Рисунок 3 - Силы, действующие на профиль в потоке
Вектор аэродинамической силы Р, действующей, например, на профиль (рис. 3), можно определить, интегрируя силы давления р и трения τ , с которыми газ действует на поверхность f этого профиля, т.е.
Однако определение силы Р интегрированием сил давления и трения газа затруднительно, т.к. значения и распределение этих сил по поверхности обтекаемого тела довольно сложно определить.
Но, если использовать теорему Эйлера об изменении количества движения газового потока при обтекании тела, то аэродинамическую силу, действующую на тело, можно определить без знания р и τ во всех точках обтекаемой поверхности.
Примем, что движение газа установившееся.
Выделим произвольной поверхностью F некоторый объем газа, окружающий обтекаемое тело, например, профиль. Такую поверхность обычно называют контрольной поверхностью . На рис. 4 показано плоское сечение этой поверхности. Отбросим газ вне контрольной поверхности и заменим его действие на газ внутри этой поверхности силами давления и трения.
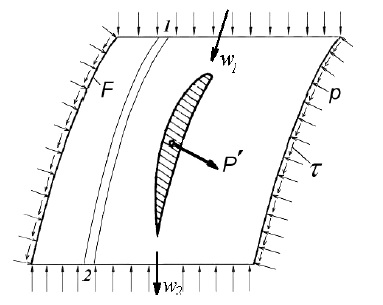
Рисунок 4 - К объяснению теоремы Эйлера
Тогда в соответствии с теоремой Эйлера при установившемся течении газа сумма всех газодинамических сил (сил давления и трения), действующих на выделенную произвольной контрольной поверхностью F массу газа со стороны отброшенного вне этой поверхности газа и обтекаемых тел, равна разности количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа, т.е.
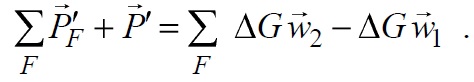
Здесь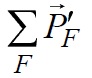 
сумма сил, действующих на массу газа, находящегося внутри контрольной поверхности со стороны самой контрольной поверхности, 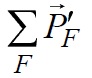сила, действующая на этот газ со стороны обтекаемого тела (профиля),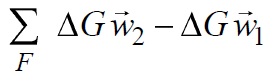 
разность количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа.
Рациональным выбором формы контрольной поверхности можно облегчить вычисление как этих газодинамических сил, так и количеств движения вытекающей и втекающей в единицу времени масс газа. Сила, действующая на обтекаемое тело (профиль), Р = –Р′ .